Multigrid Geometric Active Contours
|
||||||||||
Overview |
||||||||||
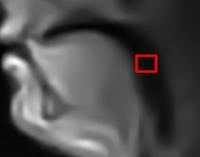
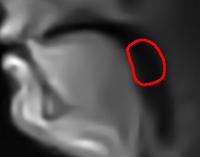
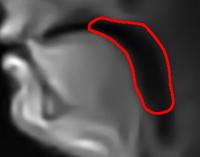
| Geometric active contour/snake models are very popular partial differential equation-based tools in image analysis and computer vision, with numerous applications such as image segmentation and moving object tracking. These models are conveniently implemented with level sets, but traditional level-set-based implementations have been notoriously slow.
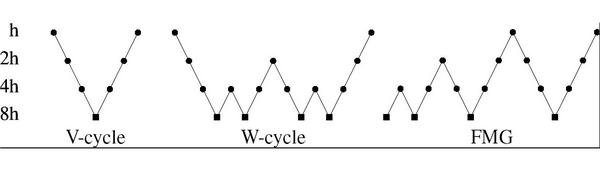
We have developed novel multigrid algorithms for the fast evolution of level-set-based geometric active contours, which allow real-time performance on conventional PCs. We overcome the main bottleneck associated with most numerical implementations of geometric active contours, namely the need for very small time steps to avoid instability, by employing a very stable fully 2-D implicit-explicit time integration numerical scheme. The proposed scheme is more accurate and has improved rotational invariance properties compared with alternative split schemes, particularly when big time steps are utilized. We then apply properly designed multigrid methods to efficiently solve the occurring sparse linear system. The combined algorithm allows for the rapid evolution of the contour and convergence to its final configuration after very few iterations. Key for the efficiency of the technique is the solution of a big sparse linear system with multigrid techniques, which attack the problem at multiple resolutions, in one of the schedules depicted on Figure 2:
The technique is applicable to a wide range of geometric active contour segmentation models; for example,
can all be solved very efficiently with the proposed method.
|
||||||||||
People |
||||||||||
Publications |
||||||||||
|
||||||||||
Software |
||||||||||
| GAC++, a C++ toolbox for geometric active contours and other related PDE-based computer vision models, implements these ideas and can be found here. | ||||||||||