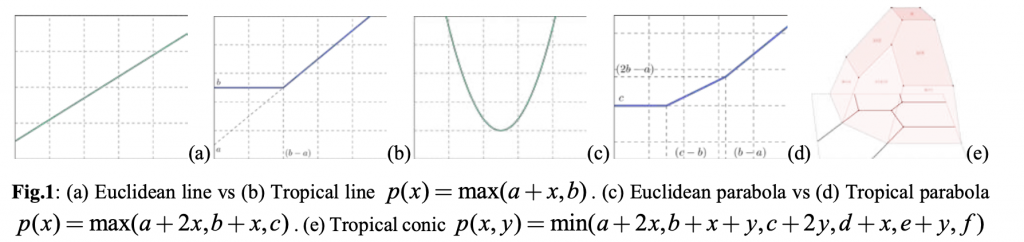
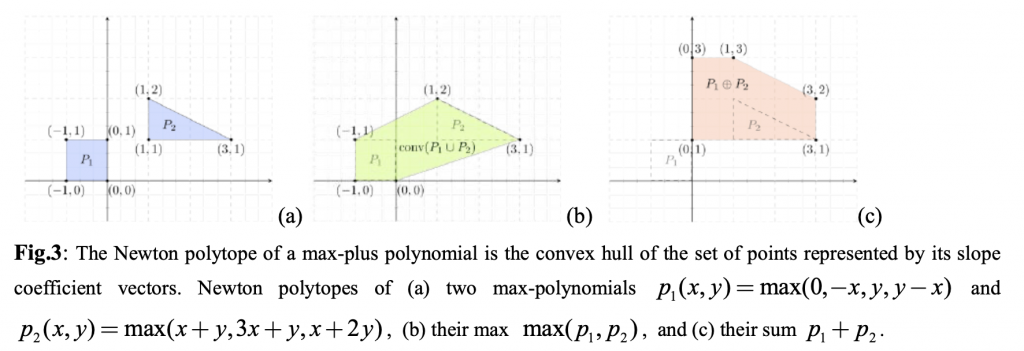
TROGEMAL

TROGEMAL: Tropical Geometry and Machine Learning

The TROGEMAL (Tropical Geometry and Machine Learning) project, led by Professor Petros Maragos at the National Technical University of Athens, aims to advance the theoretical analysis and development of machine learning systems and algorithms using tools from tropical geometry and max-plus algebra. This three-year research project explores innovative approaches in key areas such as neural networks, graphical models, and nonlinear regression.

The research focuses on four main objectives:

  1. Developing New Tropical Regression Techniques: Creating methods for data fitting using tropical polynomials and piecewise-linear (PWL) functions, with applications in multivariate nonlinear regression.
  2. Analyzing and Simplifying Neural Networks: Leveraging tropical geometry to understand and reduce the complexity of neural networks, focusing on networks with piecewise-linear activations.
  3. Applying Tropical Methods to Graphical Models and Inference Algorithms: Enhancing algorithms like the Viterbi algorithm and probabilistic graphical models by viewing them through the lens of tropical geometry.
  4. Extending Tropical Geometry to More General Algebraic Structures: Developing a generalized max-* algebra to create new frameworks for machine learning problems over weighted lattices.

By leveraging tropical geometry, the project aims to provide new insights, develop optimization algorithms, and generalize existing approaches in machine learning. The outcomes are expected to have a significant impact on both the theoretical foundations and practical applications of machine learning and artificial intelligence.

  • WP1: Tropical Regression
    • T1.1: Algorithms for Multivariate Tropical Regression with Convex PWL Models
    • T1.2: Slope transforms and Tropical Regression with General Convex Models
    • T1.3: Extensions of Tropical Regression to Non-convex PWL Models
  • WP2: Tropical Geometry of Neural Networks
    • T2.1: Tropical Geometric Analysis of NNs with PWL Activations
    • T2.2: Simplification – Minimization of Neural Networks
  • WP3: Tropical Geometry of Graphical Models & Inference Algorithms
    • T3.1: Tropical Modeling and Spectral Characterization of WFST Algorithms
    • T3.2: Tropical Geometry of Statistical Models
  • WP4: Generalized Tropical Geometry & Learning on Weighted Lattices
    • T4.1: Extensions of Tropical Geometry and Regression using Max-* Algebra
    • T4.2: Max-* generalization of inference algorithms
  • WP5: Project Management and Dissemination
    • T5.1: Management and Administration
    • T5.2: Dissemination of results
– Prof. Petros Maragos (PI, Director of IRAL and Head of CVSP Group at NTUA)
– Dr. George Retsinas (Post-Doctoral Researcher at the IRAL & CVSP Group at NTUA)
– Dr. Ioannis Kordonis (Post-Doctoral Researcher at the  IRAL & CVSP  Group at NTUA)
– Christos Garoufis (PhD student at the IRAL-CVSP Lab, NTUA, School of ECE)
– Dimitris Makropoulos (PhD student at the IRAL-CVSP Lab, NTUA, School of ECE)
– Panagiotis Mermigkas (PhD student at the IRAL-CVSP Lab, NTUA, School of ECE)
– Charalampos Vossos (PhD student at the IRAL-CVSP Lab, NTUA, School of ECE)
– Vasileios Charisopoulos (PhD student in the Dept. of Operations Research & Information Engineering at Cornell University)
– Georgios Smyrnis (PhD student in the Electrical & Computer Engineering Dept. at the University of Texas at Austin
– Emmanouil Theodosis (PhD student in Computer Science, School of Engineering & Applied Sciences atHarvard University)
– Nikolaos Tsilivis (PhD student at   New York University, Center for Data Science)

– Despina Kassianidi (Technician at the IRAL & CVSP Group at NTUA)
– Vicky Platitsa (Admin support at the IRAL & CVSP Group at NTUA)

Publications
  1. P. Maragos, V. Charisopoulos, E. Theodosis, “Tropical Geometry and Machine Learning”, Invited Paper, in Proceedings of the IEEE, (Special Issue: Machine Learning and Deep Learning), vol. 109, no. 5, pp. 728-755, May 2021. DOI: https://doi.org/10.1109/JPROC.2021.3065238 . [pdf]
  2. P. Misiakos, G. Smyrnis, G. Retsinas and P. Maragos, “Neural Network Approximation based on Hausdorff distance of Tropical Zonotopes”, Proc. 10th International Conference on Learning Representations (ICLR 2022), Apr. 2022. [pdf]
  3. G. Retsinas, G. Sfikas, P.P. Filntisis, and P. Maragos, “Newton-Based Trainable Learning Rate”, Proc. 48th IEEE Int’l Conf. on Acoustics, Speech and Signal Processing (ICASSP 2023), Rhodes, Greece, June 2023. [pdf]
  4. A. Glentis-Georgoulakis, G. Retsinas and P. Maragos, “Feather: An Elegant Solution to Effective DNN Sparsification”, Proc. 34th British Machine Vision Conference (BMVC), Aberdeen, UK, Nov. 2023. [pdf]
  5. I. Kordonis, E. Theodosis, G. Retsinas, and P. Maragos, “Matrix Factorization in Tropical and Mixed Tropical-Linear Algebras”, Proc. 2024 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP 2024), Seoul, Korea, April 2024. [pdf]
  6. I. Kordonis and P. Maragos, “Revisiting Tropical Polynomial Division: Theory, Algorithms, and Application to Neural Networks”, IEEE Transactions on Neural Networks and Learning Systems, 2025, DOI: https://doi.org/10.1109/TNNLS.2025.3570807. [pdf]
  7. K. Fotopoulos, C. Garoufis and P. Maragos, “Sparse Hybrid Linear-Morphological Networks”, Proceedings of  33rd European Signal Processing Conference (EUSIPCO 2025), Isola delle Femmine – Palermo, Italy, Sep. 2025. [pdf]
  8. K. Fotopoulos, P. Maragos, P. Misiakos, “TropNNC: Structured Neural Network Compression Using Tropical Geometry”, https://arxiv.org/abs/2409.03945, [pdf]
  9. K. Fotopoulos and P. Maragos, “Training Deep Morphological Neural Networks as Universal Approximators”, https://arxiv.org/abs/2505.09710, [pdf]
  10. P. Maragos, V. Charisopoulos, G. Smyrnis and E. Theodosis, Tropical Geometry and Machine Learning, Book under preparation
Invited Talks and Tutorials
  1. P. Maragos, IEEE Tutorial Course on “Introduction to Tropical Geometry and Its Applications to Machine Learning”, given at the 2022 IEEE 14th Image, Video, and Multidimensional Signal Processing Workshop (IVMSP 2022), Nafplio, Greece, June 2022. [Slides]
  2. P. Maragos, “Introduction to Tropical Geometry and its Applications to Machine Learning”, Archimedes Workshop, Athena Research Center, Athens, Greece, 18 July 2022.
  3. P. Maragos, “Tropical Geometry and Machine Learning”, University of Southern California, Dept. ECE and Ming Hsieh Institute, Los Angeles, 01 Dec. 2023.
  4. P. Maragos, IEEE Tutorial Course on “Tropical Geometry for Machine Learning and Optimization”, given at the 2024 IEEE 49th Int’l Conference on Acoustics, Speech and Signal Processing (ICASSP 2024), Seoul, Korea, April 2024. [Slides]
  5. P. Maragos, “Tropical Geometry for Machine Learning”, Plenary Talk, CaLISTA Workshop on Geometry-Informed Machine Learning, Paris, 02 Sep. 2024. [Slides]
  6. P. Maragos, “Tropical Geometry and its Applications to Machine Learning”, Mathematics & Machine Learning Seminar, Max-Planck Institute (MIS) and University of California at Los Angeles, 19 Dec. 2024.
  7. P. Maragos, “Tropical Algebra and Geometry for Machine Learning and Optimization”, Invited talk given at AIDA Symposium & Summer School on AI/ML Cutting Edge Trends (AIDA AICET2025), Aristotle Univ. of Thessaloniki, Greece, 16 July 2025.
  8. P. Maragos, Tutorial on “Tropical Algebra and Geometry for Machine Learning and Optimization” given at the 33rd European Signal Processing Conference (EUSIPCO 2025), Isola delle Femmine – Palermo, Italy, September 2025. [slides]

Project Details

The research project is supported by the Hellenic Foundation for Research and Innovation (H.F.R.I.) under the “2nd Call for H.F.R.I. Research Projects to support Faculty Members & Researchers” (Project Number:2656).
2025-09-18T11:51:21+00:00
© Copyright 2018 -    |   IRAL   |   All Rights Reserved